ロボットのデカルト座標値算出方法
Dobot CRシリーズのデカルト座標算出は修正DH法に基づいて演算されています。
演算に仕様されるパラメータは “\\192.168.5.1\project\properties\structure.json”に記述されているkey “strucure”の要素 ”L1″~”L7″(単位mm), “a1″~”a6″(単位mm), “alpha1″~”alpha6″(単位°)を参照しています。
但し、TrueMotion設定が”Open“の時は、上記のパラメータが反映されますが、”Close“の時は一部のパラメータは反映されません。
- “Close”の時は 0 となるパラメータ
- L2, L3, L7
- a1, a4, a5
- alpha2, alpha3, alpha6
- “Close”の時は 90 となるパラメータ
- alpha1, alpha4
- “Close”の時は -90 となるパラメータ
- alpha5
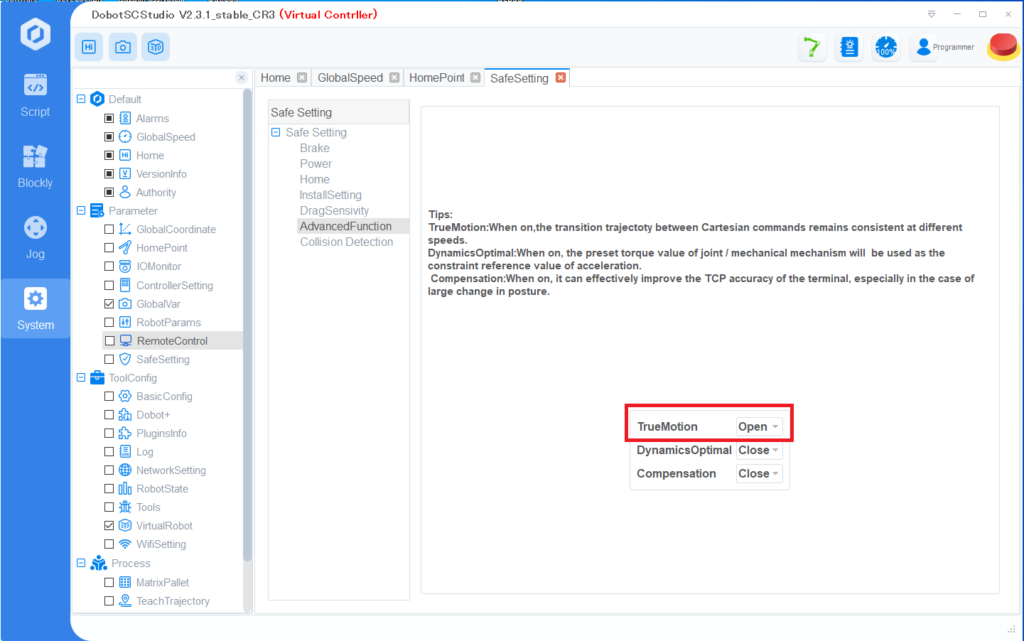
SafeSetting → AdvancedFunction
structure.jsonファイル内のパラメータ記述部と修正DH法での各座標配置を参考にしてください。
"structure": {
"L1": 134.8000030517578,
"L2": 0,
"L3": 0,
"L4": 128.35633850097656,
"L5": 116.11260986328125,
"L6": 105,
"L7": 0,
"a1": 0.6618859767913818,
"a2": -274.5413818359375,
"a3": -230.2163848876953,
"a4": 0.06995099782943726,
"a5": -0.32764101028442383,
"a6": 0,
"alpha1": 90.06243133544922,
"alpha2": -0.024058999493718147,
"alpha3": -0.1476230025291443,
"alpha4": 90.05494689941406,
"alpha5": -90.06172180175781,
"alpha6": 0,
"armSingularity12": 10,
"elbowSingularity12": 2,
"limits": [[-357,357],
[-178,178],
[-155,155],
[178,178],
[-178,178],
[-357,357]],
"wristSingularity12": 2
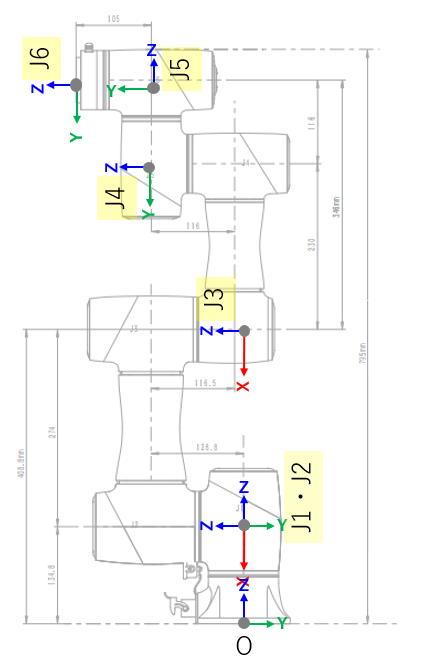
} 各ジョイントにおける基準座標原点位置
座標原点は各ジョイントの回転軸上であればどこにでも配置できますが、前述のロボットコントローラーに記憶されているDHパラメーターをそのまま使用できるよう配置しています。
ソースコード
順運動学の考えによりジョイント角度からエンドエフェクタの座標を計算するコードです。
行列の計算にはEigenライブラリを使用しています。
#include <iostream>
#include <format> C++20以降
#include <Eigen/Dense>
const double PI = 3.1415926535;
//ジョイント情報構造体
struct JointValues
{
double J1;
double J2;
double J3;
double J4;
double J5;
double J6;
void Set(double j1, double j2, double j3, double j4, double j5, double j6) {
J1 = j1;
J2 = j2;
J3 = j3;
J4 = j4;
J5 = j5;
J6 = j6;
}
};
//座標情報構造体
struct Coordinate
{
double x;
double y;
double z;
double rx;
double ry;
double rz;
void Set(double x0, double y0, double z0, double rx0, double ry0, double rz0) {
x = x0;
y = y0;
z = z0;
rx = rx0;
ry = ry0;
rz = rz0;
}
};
//DHパラメーター構造体
struct DHParameter
{
double Alpha;
double A;
double OriginTheta;
double D;
void Set(double alpha, double a, double zero, double d) {
Alpha = alpha;
A = a;
OriginTheta = zero;
D = d;
}
};
//同次変換行列を取得する
void GetTFMatrix(Eigen::Matrix4d& mat, DHParameter param, double jointValue) {
double theta = param.OriginTheta + jointValue;
mat(0, 0) = std::cos(theta * PI / 180);
mat(0, 1) = -std::sin(theta * PI / 180);
mat(0, 2) = 0;
mat(0, 3) = param.A;
mat(1, 0) = std::cos(param.Alpha * PI / 180) * std::sin(theta * PI / 180);
mat(1, 1) = std::cos(param.Alpha * PI / 180) * std::cos(theta * PI / 180);
mat(1, 2) = -std::sin(param.Alpha * PI / 180);
mat(1, 3) = -param.D * std::sin(param.Alpha * PI / 180);
mat(2, 0) = std::sin(param.Alpha * PI / 180) * std::sin(theta * PI / 180);
mat(2, 1) = std::sin(param.Alpha * PI / 180) * std::cos(theta * PI / 180);
mat(2, 2) = std::cos(param.Alpha * PI / 180);
mat(2, 3) = param.D * std::cos(param.Alpha * PI / 180);
mat(3, 0) = 0;
mat(3, 1) = 0;
mat(3, 2) = 0;
mat(3, 3) = 1;
}
//同次変換行列からオイラー角を取得する
Eigen::Vector3d GetEulerAngle(Eigen::Matrix4d rot)
{
double phi, theta, psi;
theta = std::asin(-rot(2, 0));
//ジンバルロック
if (std::abs(theta - PI / 2) < 0.000001 || std::abs(theta + PI / 2) < 0.000001)
{
//ジンバルロック時はrx=0とする。
phi = 0;
psi = -std::atan2(rot(0, 1), rot(1, 1));
}
else
{
//cos(theta)>0は常に成立
phi = std::atan2(rot(2, 1), rot(2, 2));
psi = std::atan2(rot(1, 0), rot(0, 0));
}
if (std::abs(phi - (-PI)) < 0.00001)
phi = PI;
if (std::abs(psi - (-PI)) < 0.00001)
psi = PI;
Eigen::Vector3d v(phi, theta, psi);
return v;
}
//ジョイント角度からエンドエフェクタ座標を取得する
void ComputeFK(JointValues jointValues, std::array<DHParameter, 6>dhParameters,
Coordinate& eefectorCoordinate)
{
std::array < Eigen::Matrix4d, 6> tfMatrices{};
for (int i = 0; i < 6; i++) {
double val;
switch (i)
{
case 0:
val = jointValues.J1;
break;
case 1:
val = jointValues.J2;
break;
case 2:
val = jointValues.J3;
break;
case 3:
val = jointValues.J4;
break;
case 4:
val = jointValues.J5;
break;
case 5:
val = jointValues.J6;
break;
}
GetTFMatrix(tfMatrices[i], dhParameters[i], val);
}
Eigen::Matrix4d mat;
for (int i = 0; i < 6; i++)
{
if (i == 0)
mat = tfMatrices[0];
else
mat = mat * tfMatrices[i];
}
eefectorCoordinate.x = mat(0, 3);
eefectorCoordinate.y = mat(1, 3);
eefectorCoordinate.z = mat(2, 3);
Eigen::Vector3d euler = GetEulerAngle(mat);
eefectorCoordinate.rx = euler.x() * 180 / PI;
eefectorCoordinate.ry = euler.y() * 180 / PI;
eefectorCoordinate.rz = euler.z() * 180 / PI;
}
//実行関数
int main()
{
std::array<DHParameter, 6> dhParameters{};
//DHパラメーターを入力 ロボットに合わせて入力
dhParameters[0].Set(0, 0, 0, 134.8);
dhParameters[1].Set(90, 0, -90, 0);
dhParameters[2].Set(0, -274.541, 0, 0);
dhParameters[3].Set(0, -230.216, -90, 128.356);
dhParameters[4].Set(90, 0, 0, 116.113);
dhParameters[5].Set(-90, 0, 0, 105);
JointValues jointValues{};
jointValues.Set(10, 30, 90, -20, -85, 10);
Coordinate coord{};
ComputeFK(jointValues, dhParameters, coord);
std::cout << "J1:" << std::format("{:f}", jointValues.J1) << std::endl;
std::cout << "J2:" << std::format("{:f}", jointValues.J2) << std::endl;
std::cout << "J3:" << std::format("{:f}", jointValues.J3) << std::endl;
std::cout << "J4:" << std::format("{:f}", jointValues.J4) << std::endl;
std::cout << "J5:" << std::format("{:f}", jointValues.J5) << std::endl;
std::cout << "J6:" << std::format("{:f}", jointValues.J6) << std::endl<< std::endl;
std::cout << "X:" << std::format("{:f}", coord.x) << std::endl;
std::cout << "Y:" << std::format("{:f}", coord.y) << std::endl;
std::cout << "Z:" << std::format("{:f}", coord.z) << std::endl;
std::cout << "Rx:" << std::format("{:f}", coord.rx) << std::endl;
std::cout << "Ry:" << std::format("{:f}", coord.ry) << std::endl;
std::cout << "Rz:" << std::format("{:f}", coord.rz) << std::endl;
}実行結果
J1:10.000000
J2:30.000000
J3:90.000000
J4:-20.000000
J5:-85.000000
J6:10.000000
X:-402.375169
Y:-210.578224
Z:134.277342
Rx:169.269479
Ry:3.116937
Rz:89.269479